分散分析(平均の差の検定)
SPSS Statisticsによる実践解説
教育によって収入に差があるのか、SPSSで分散分析をしてみた
教育は個人の収入に大きな影響を与える要因の一つです。一般的には、高い学歴を持つ人ほど高収入を得る傾向にあるとされています。しかし、この関係は一様ではなく、他の要因(地域、職業、産業など)も関与してきます。そこで、分散分析などの平均の差を検定することで、教育と収入の関係が統計的に有意であるかどうかを検証することができます。
分散分析とは
分散分析(Analysis of Variance, ANOVA)は、複数のグループ間で平均値に統計的に有意な差があるかどうかを検証するための統計手法です。この手法は、グループ間の変動とグループ内の変動を比較することで、グループ間の差異が偶然によるものか、他の要因によるものかを判断します。
当コラムではSPSS Statistics を使って、以下のように順を追って実施していくことで様々な角度から検証をしていきます。
- データの確認、外れ値除去
- 各グループの平均値の確認
- 各グループのデータの分布を箱ひげ図で確認
- t検定(2グループの平均の差の検定)
- 分散分析(複数グループの平均の差の検定)
今回使用するデータは下記のようなデータです。
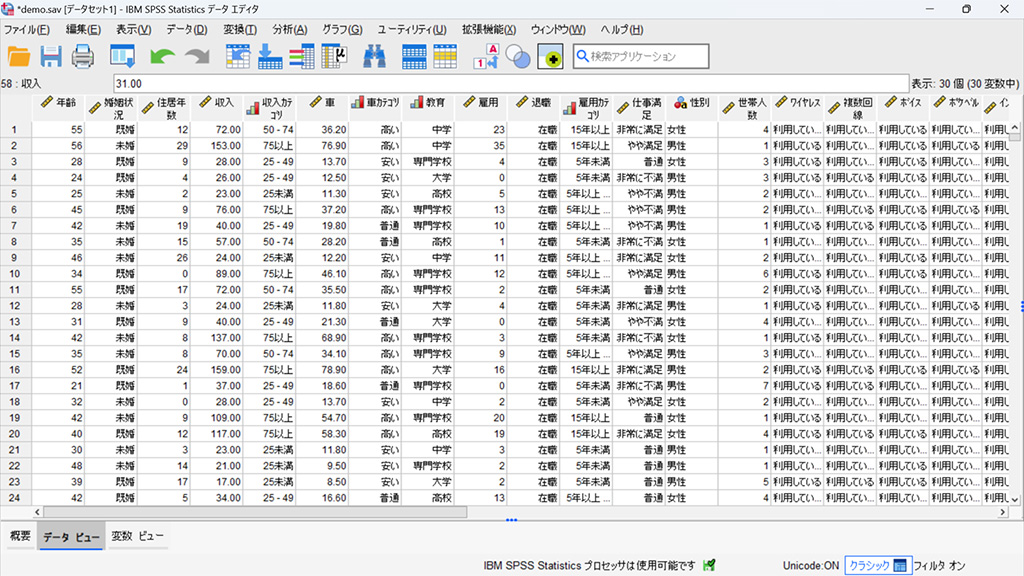
データの確認、外れ値除去
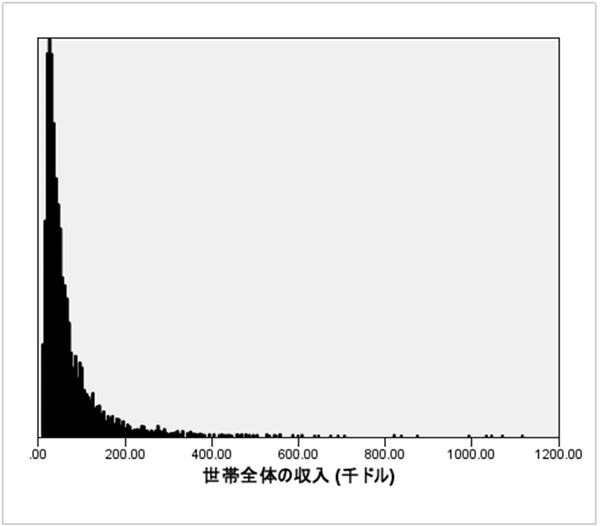
分析を始める前にデータを絞り込んだり尺度を変更して、分析を行いやすいように準備をします。世帯全体の収入のヒストグラムを見ると長い尾を引いたグラフになっていて外れ値が多いことが確認できます。このような外れ値は平均などの値に大きな影響を与えてしまうので分析から除外することがあります。今回は世帯全体の収入が200,000ドル以上のデータは分析から除外することにします。
※ヒストグラムは 「グラフ」メニュー のヒストグラムからご確認いただけます。
外れ値除去 手順
1.SPSS Statisticsを起動し、編集メニュー 「データ」メニュー からケースの選択、を選択。
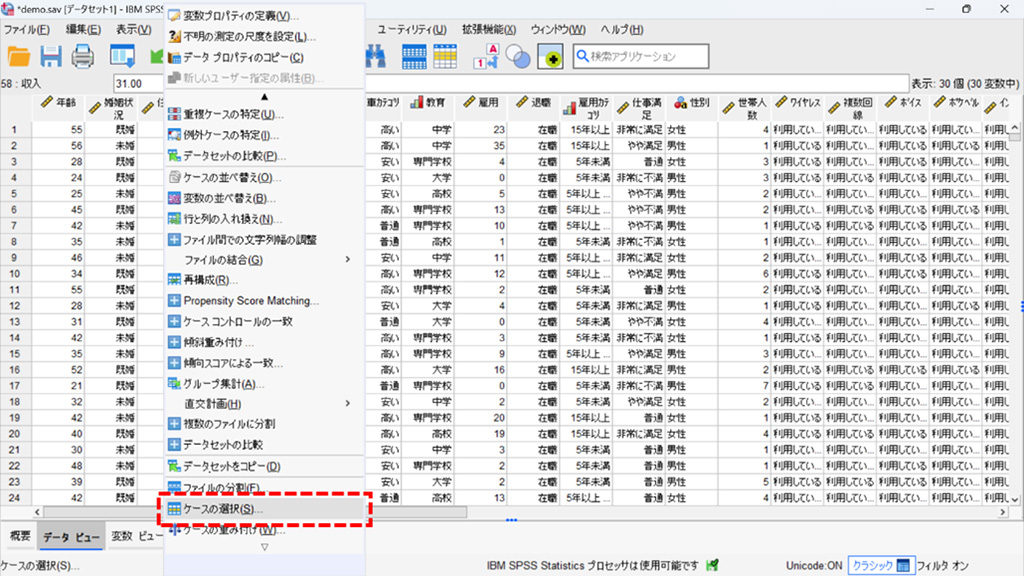
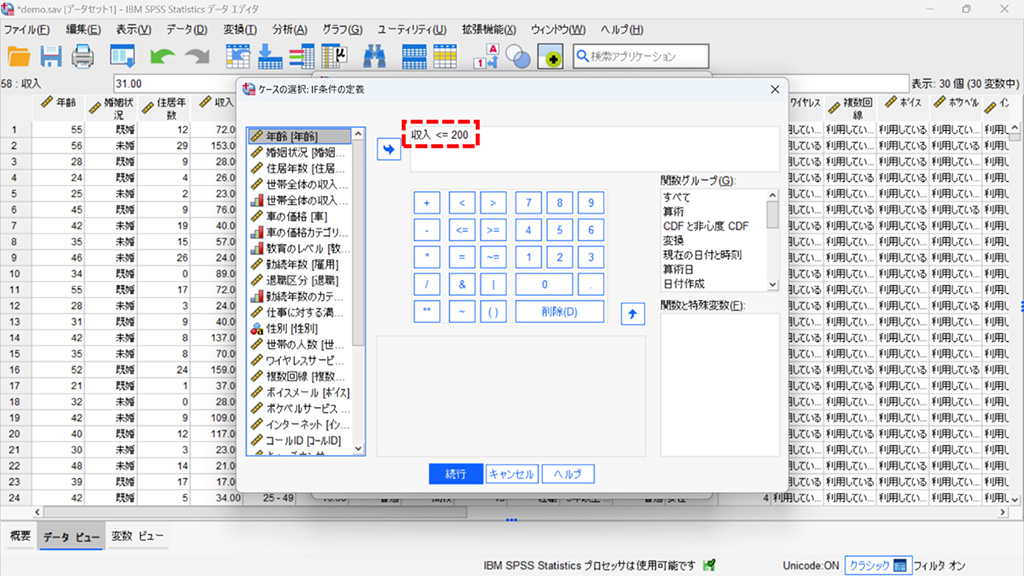
2.IF条件が満たされるケースを選択しIFのボタンをクリックします。
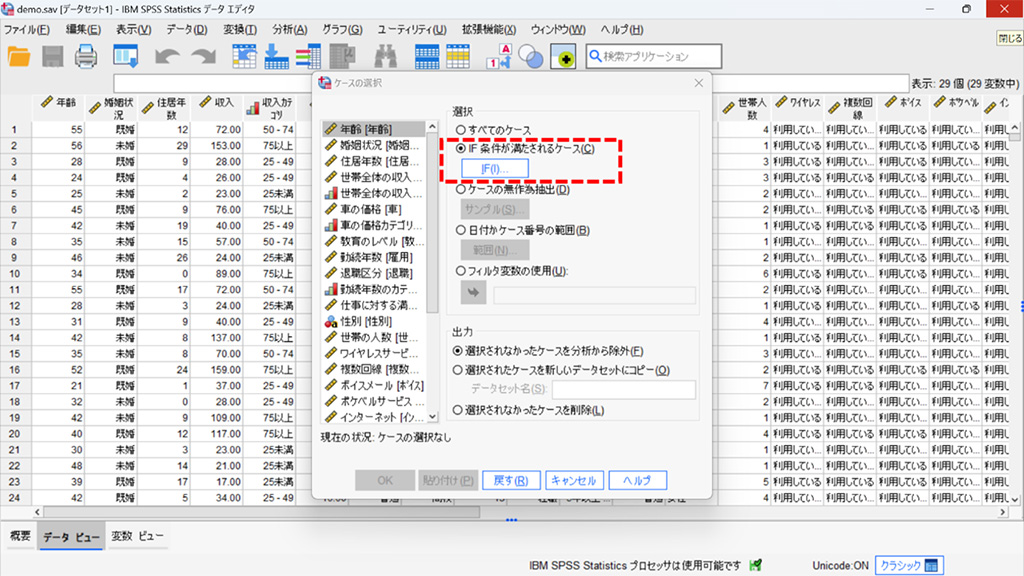
3.式に 「収入<=200」 と入力します。
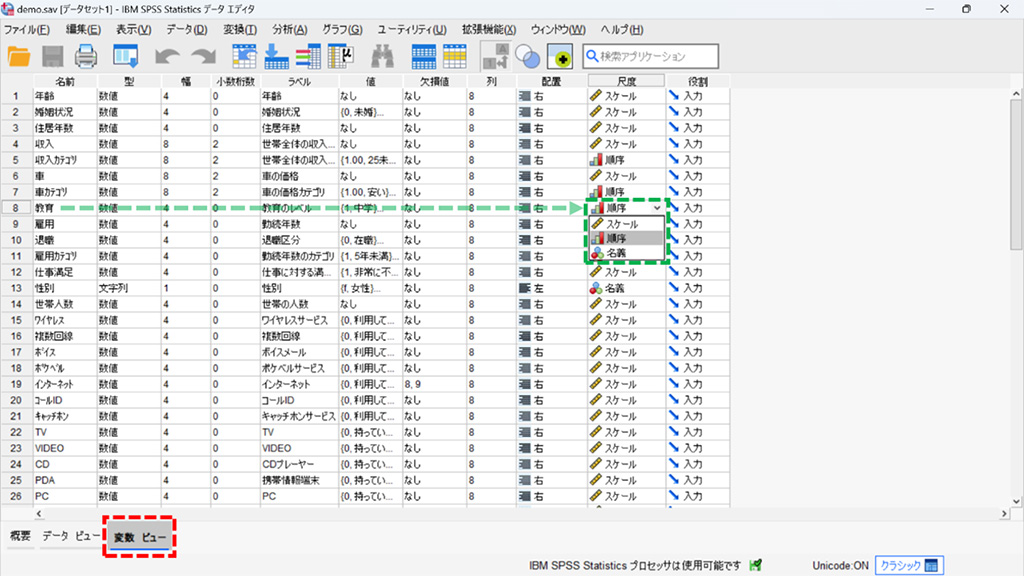
4.タブをデータビューから変数ビューに切り替えます。
5.「教育」 の尺度をスケールから順序に切り替えます。
それでは早速分析に進んでいきましょう。
各グループの平均値の確認
手順
1.「分析」メニュー から平均値と比率の比較、そしてグループの平均を選択。
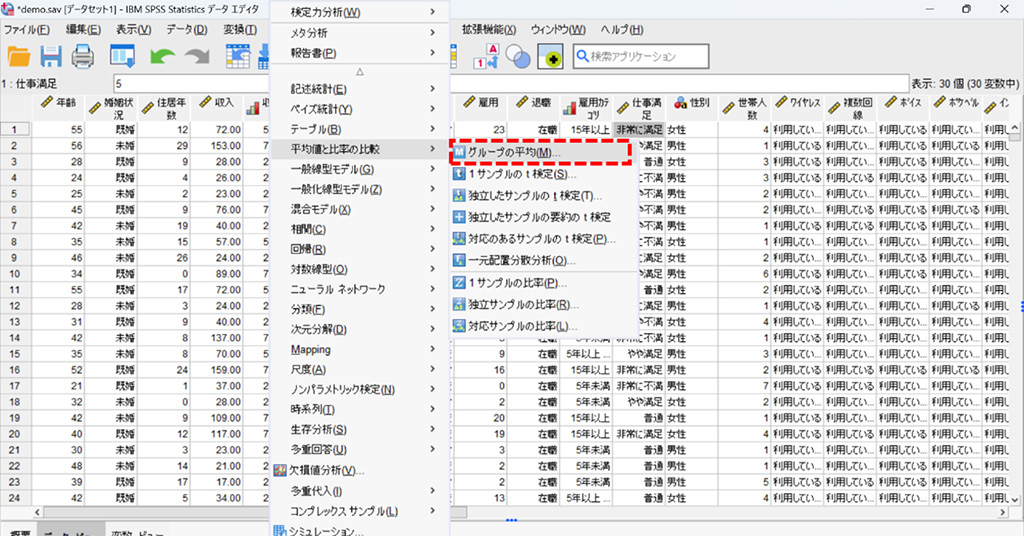
2.**従属変数リスト**に「世帯全体の収入」を、**独立変数**に「教育のレベル」を設定。
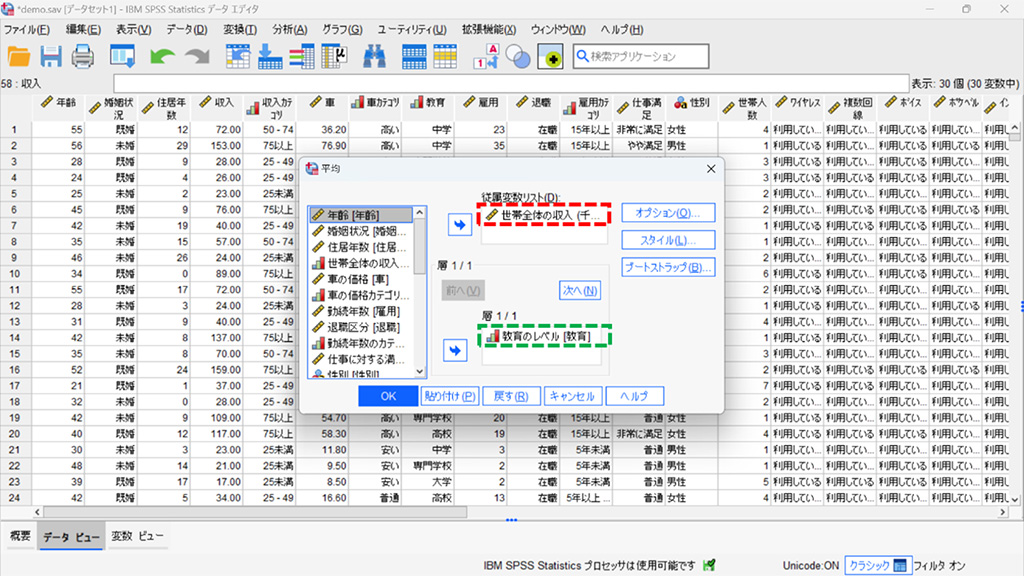
結果の確認
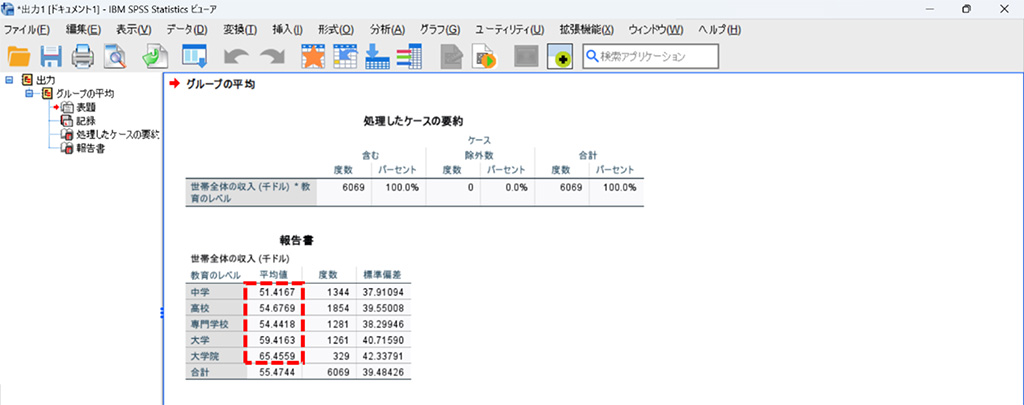
中学、高校、大学、大学院と教育レベルが上がるにつれて世帯収入も上がっていくことが確認できます。
各グループのデータの分布を箱ひげ図で確認
今度は箱ひげ図を用いてデータの分布を視覚的に表現してみましょう。
手順
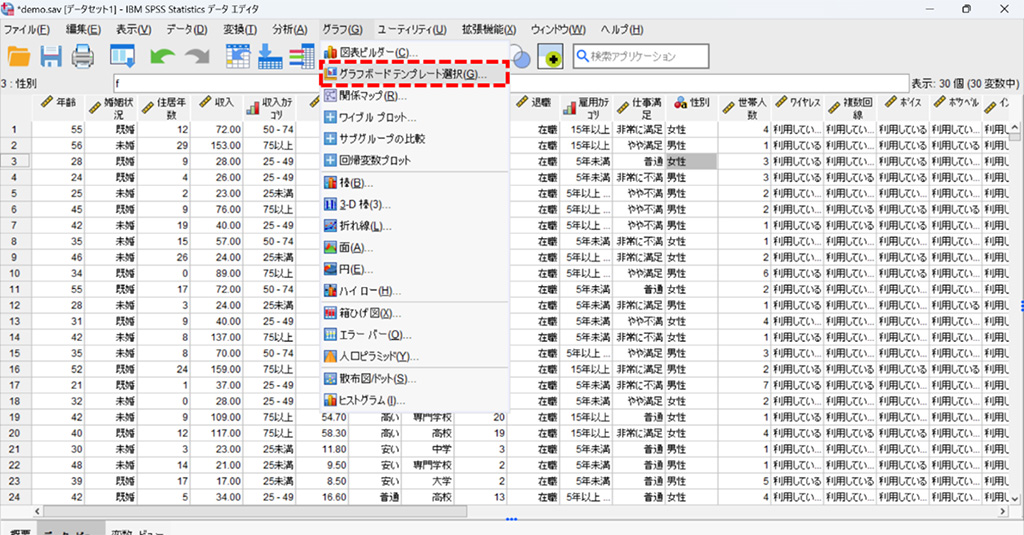
1.「グラフ」メニューからグラフボードテンプレートを選択。
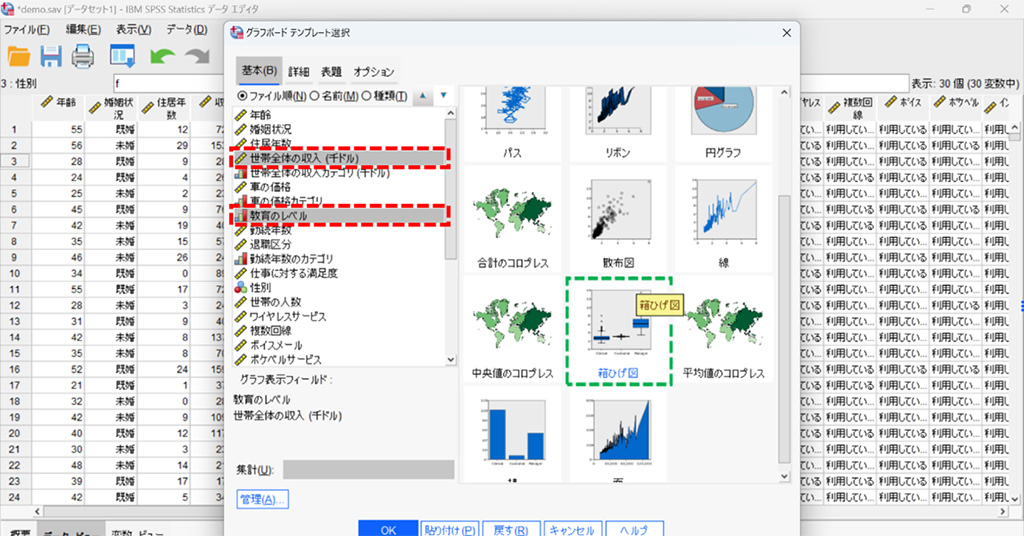
2.世帯全体の収入 と 教育のレベル を同時に選択し右側の 箱ひげ図 をクリック。
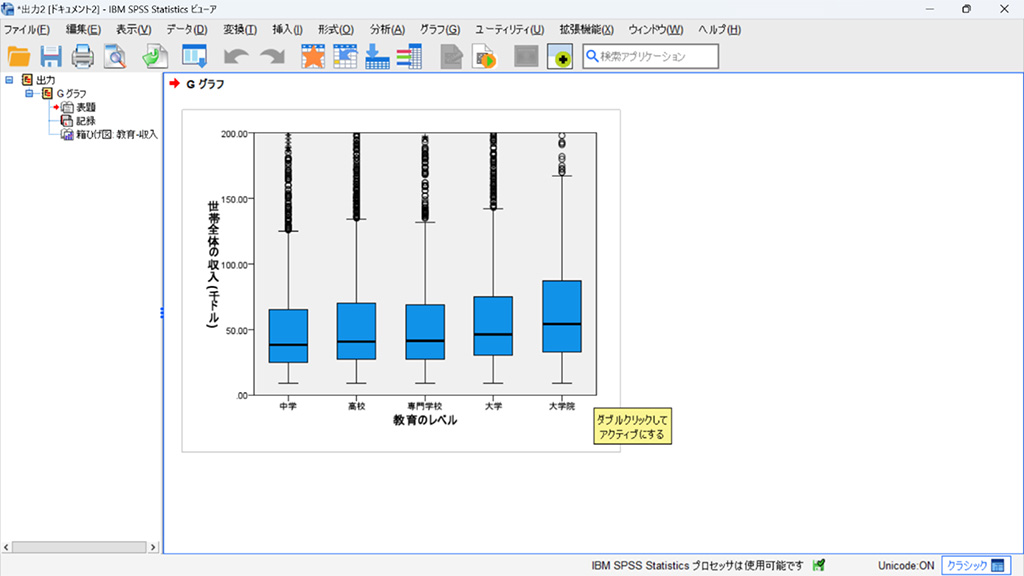
結果の確認
箱ひげ図で視覚的に確認すると大学院はほかの4つと比べて世帯収入が高い印象がありますね。
箱ひげ図(Box Plot)の解説
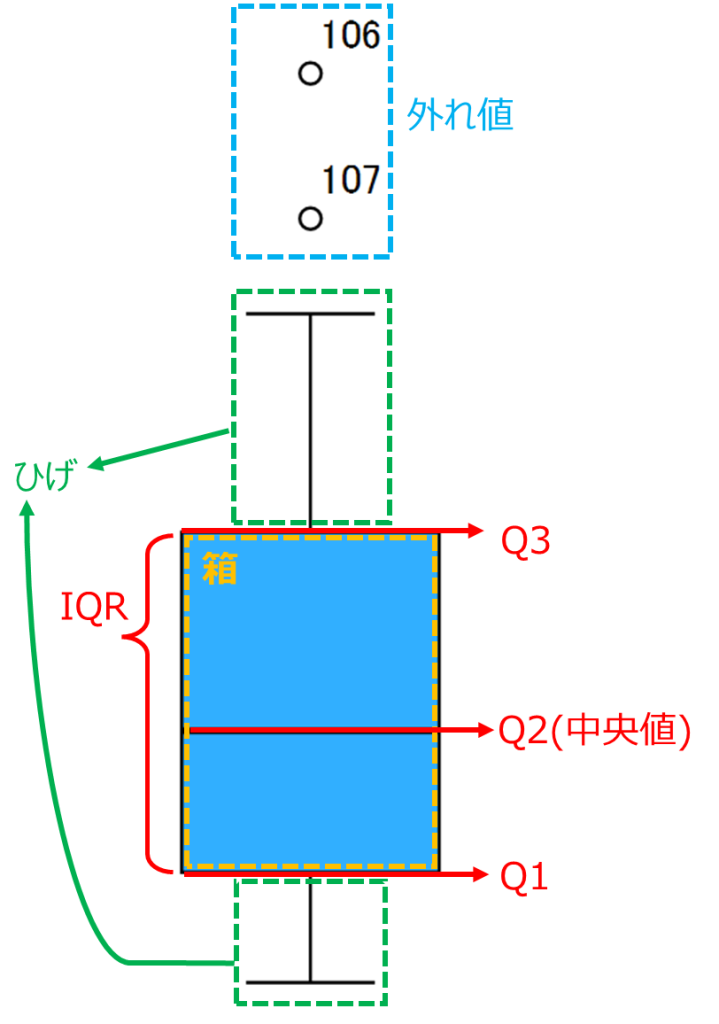
箱ひげ図(Box Plot)は、データの分布を視覚的に表現するためのグラフです。データの中央値や四分位範囲、最小値、最大値、及び外れ値を示すことで、データの特性を一目で理解することができます。
箱ひげ図の構成要素
1.箱(ボックス):
- 第1四分位数(Q1):データの下位25%の境界。箱の下端に位置します。
- 第3四分位数(Q3):データの上位25%の境界。箱の上端に位置します。
- 四分位範囲(IQR):Q1からQ3までの範囲で、データの中央50%を示します。
2.中央値(第2四分位数、Q2):
- 箱の中の線で示され、データの中心点を表します。データを2つの等しい部分に分ける値です。
3.ひげ(ウィスカー):
- 箱の上下に伸びる線で、データの範囲を示します。
- 通常、ひげの範囲は「Q1 – 1.5 × IQR」から「Q3 + 1.5 × IQR」の範囲内に収まるデータを含みます。
4.外れ値(アウトライア):
- ひげの範囲外に位置するデータポイントで、一般的には「Q1 – 1.5 × IQR」より小さいか「Q3 + 1.5 × IQR」より大きい値で個別に点で示されます。
- 極値は「Q1 – 3 × IQR」より小さいか「Q3 + 3 × IQR」より大きい値で*(アスタリスク)で示されます。
2グループ平均の差の検定(対応なしt検定)
男性、女性等の性別によって世帯収入に差があるかどうか調べてみましょう。
手順
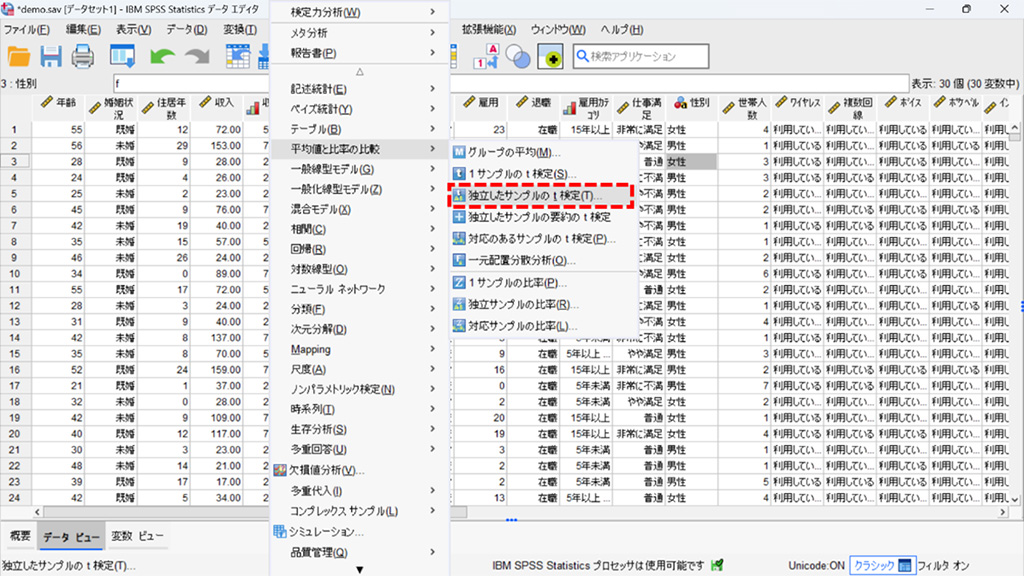
1.「分析」メニューから平均値と比率の比較、そして独立したサンプルのt検定を選択。
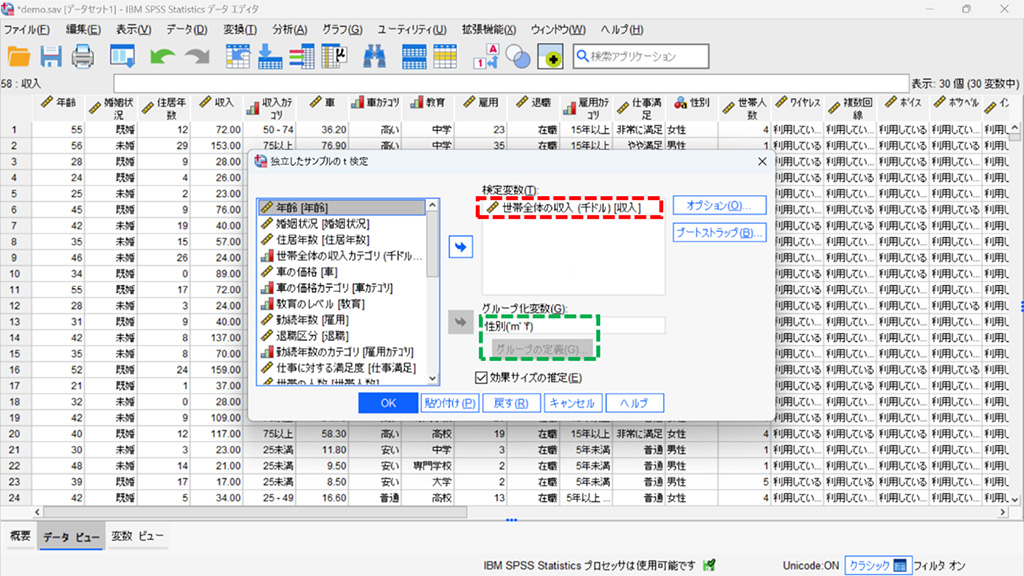
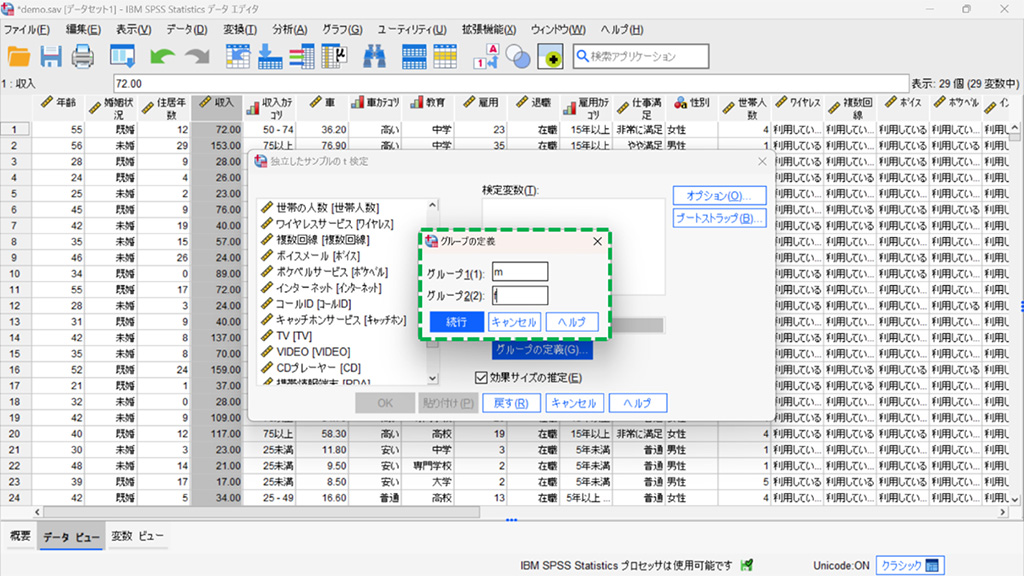
2.**検定変数 **に「世帯全体の収入」を、**グループ化変数 **に「性別」を設定。
結果の確認
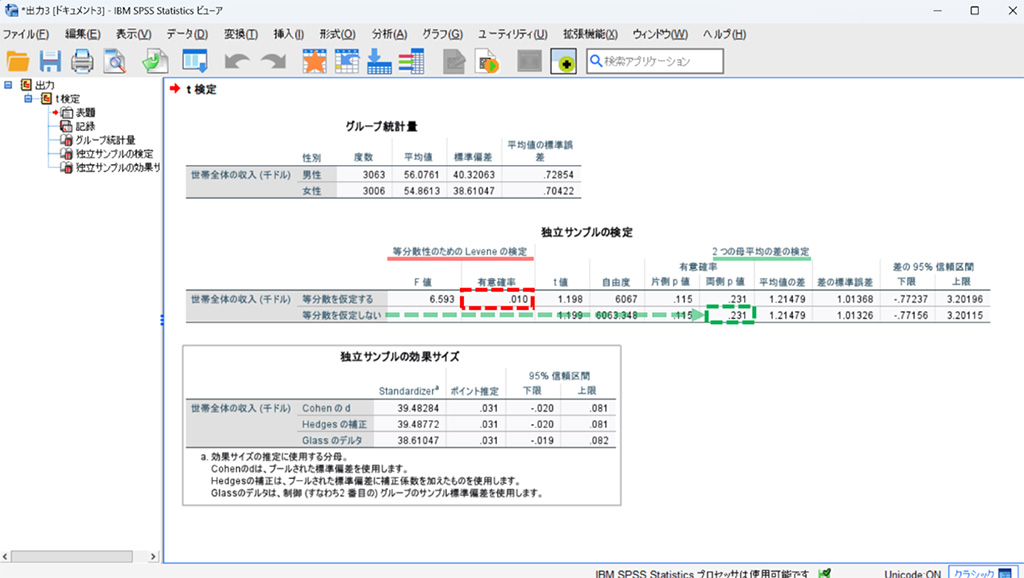
グループ統計量を確認すると男性の方が平均が高いです。しかしこの差は統計的に有意なのでしょうか。もう少し詳しくみてみましょう。独立サンプルの検定の欄で「等分散性のためのLeveneの検定」を見ると有意確率が0.01で0.05を下回っているので分散が有意に異なるといった結果になります。したがって「等分散を仮定しない」の行を見ることにします。「二つの母平均の差の検定」を見ると両側検定の値(両側p値)が0.05を上回っているので有意な差はないと判断できます。つまり男性と女性の収入の平均に有意な差はないことになります。
一元配置分散分析
単一の独立変数(要因)に対して、複数のグループの平均値を比較する手法です。
教育のレベルによって世帯収入に統計的に有意な差があるかどうか確認してみましょう。
手順
3.「分析」メニューから平均値と比率の比較、そして一元配置分散分析を選択。
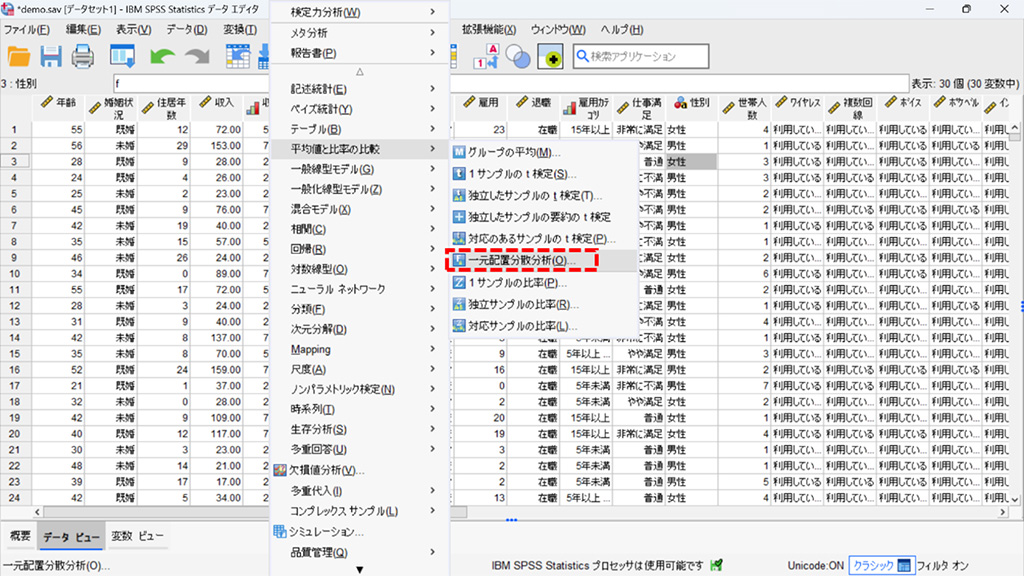
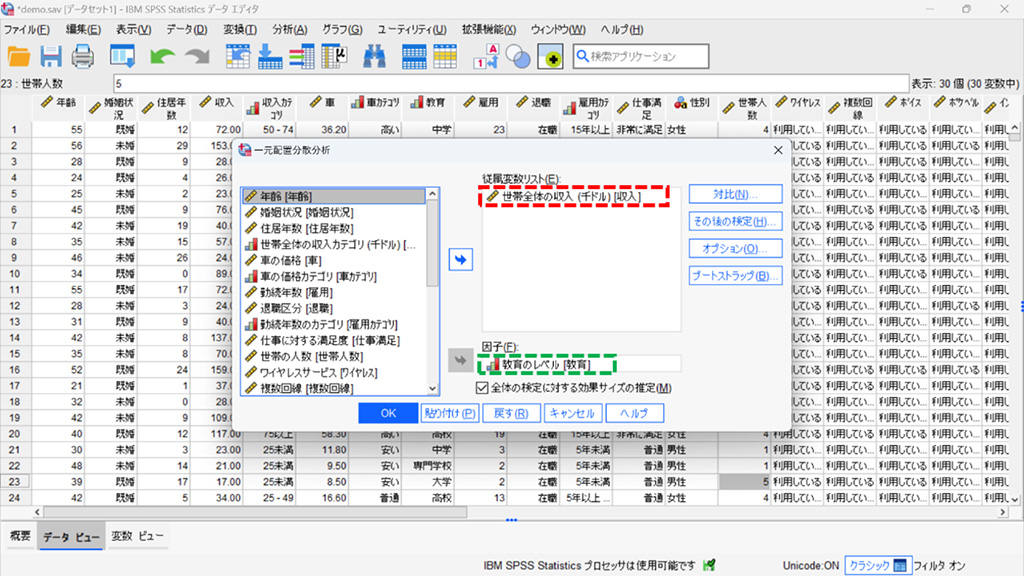
4.**従属変数リスト**に「世帯全体の収入」を、**因子 **に「教育のレベル」を設定。
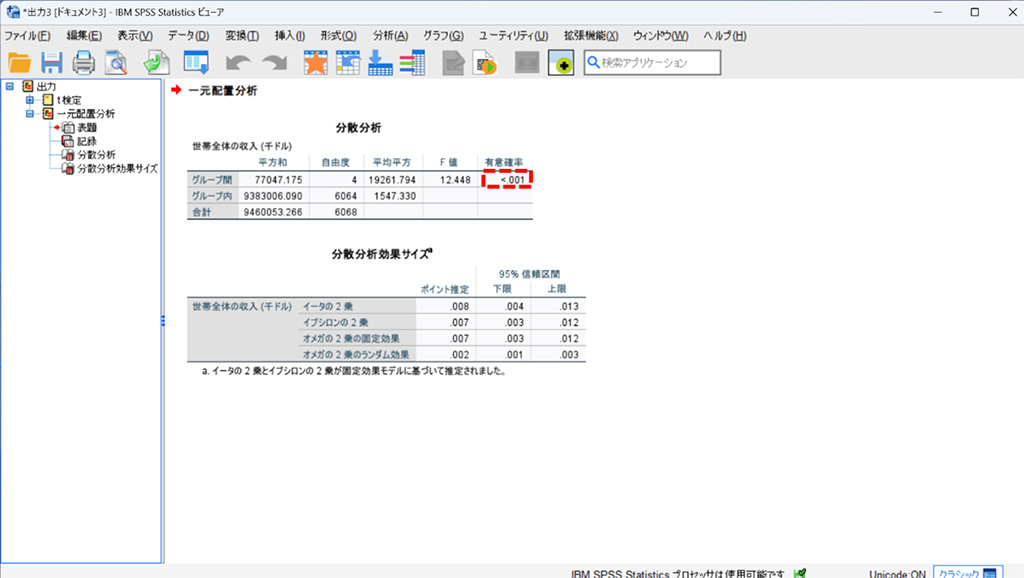
結果の確認
分散分析の有意確率を見ると0.05未満なので有意な差があると判断できます。
まとめ
分散分析は、複数のグループ間の平均値の差を統計的に評価するための強力なツールです。この手法を正しく理解し、適切に適用することで、データに基づいた客観的な判断を行うことが可能になります。分散分析をマスターすることで、データ分析のスキルを一段と向上させることができるでしょう。
企業活動における分析対象は、企業内に蓄積されたデータのみならず、Webサイト上など社外の公開データ、さらにはSNSなどの外部データも含め、非常に多岐にわたるものとなっています。このため、社内外に蓄積された各種のデータを基に、透過的、そして一貫した形で予測分析を実現できる仕組みやサービスが求められています。 AITでは、分析プロジェクトの検討段階から、データ準備の支援、モデル開発、ビジネス活用、また人材育成までをトータルにご支援。お客様ご自身が継続的なデータ分析活動を推進できる組織、体制作りのお手伝いをします。お気軽にご相談ください。
