線形回帰分析とは?
活用例から使い方、単回帰分析と重回帰分析の違いまで解説
昔から最もよく使われてきた分析手法のひとつが「回帰分析」です。例えば、高校の入学試験の成績と入学後の試験の成績は、どのように関係しているのか知りたいといった場合に、変数間の関係を推測するために回帰分析が用いられます。その回帰分析の中で主流なのが「線形回帰分析」です。本コラムでは、線形回帰分析の基本から使い方、活用例までわかりやすく解説します。
1.線形回帰分析の活用例
線形回帰分析について詳しく解説する前に、まずは線形回帰分析がビジネスでどのように応用されているのか活用例を見ていきましょう。
小売業やWebショップ、金融業など幅広い分野で、売上や需要などを予測するために線形回帰分析が使用されています。原因と考えられる情報をインプットして予測モデルを作成。将来の予測値を算出し、売上を増やすための要因を特定したり、需要に対応できるよう対策を打ったりしています。
製造業においては、製造過程の条件をインプットとして、故障や不良品発生を表す異常な数値の要因を特定するのに線形回帰分析を使っています。
2.線形回帰分析とは
線型回帰分析とは、2つ以上の量的変数間の関係を直線的な(線形)式で表す手法です。英語だと「linear regression analysis」と書きます。
売上や出荷数などの予測したい情報を「目的変数(従属変数)」、売上や出荷数が増えたり減ったりする原因と考えられる情報を「説明変数(独立変数)」などと呼びます。
線形回帰分析は、あくまでも直線的な関係のみをモデルにとらえ(線形の関係のみで、曲線的な関係ではない)、目的変数(y)に説明変数(x)がどれだけ影響を与えるかを予測する方法です。
3.線形回帰分析の種類:単回帰分析と重回帰分析の違い
線形回帰分析は、大きく分けて「単回帰分析」と「重回帰分析」に分けられます。それぞれの違いを見ていきましょう。
単回帰分析
1つの説明変数(x)によって1つの目的変数(y)を予測し、一次方程式(y=ax+b)の形で表せるものを単回帰分析といいます。
例えば、カフェをどういった場所に出店すると、出店後1年目でどれくらいの売上が見込めるか予測する場合を考えてみましょう。
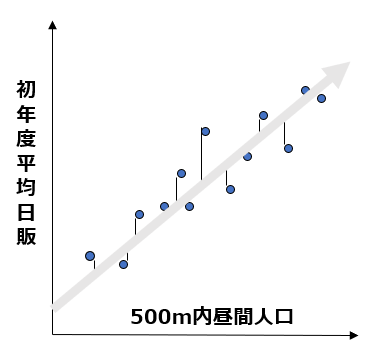
上図は、半径500m以内の昼間人口に対するカフェの初年度の平均日販データになります。ドットは実測値です。この各データからの距離がもっとも小さくなるような直線を引きます。カフェの初年度平均日販を目的変数y、500m内昼間人口を説明変数xとすると、次の数式が導き出されます。

つまり500m内昼間人口1人あたりの影響度は約19円になります。仮に500m内昼間人口を1万人に設定した場合、日販は約19円×1万人+31.6万円=50.6万円です。
このように、一次方程式で算出すると予測値を算出できます。ただし当然のことながら、実際の売上と完全に一致する訳ではありません。一般に単回帰分析の式で算出された予測値は、誤差が大きく精度が低い傾向にあります。
重回帰分析
重回帰分析とは、2つ以上の説明変数(x)によって1つの目的変数(y)を予測し、一次方程式の形で表わせるものを指します。
先ほどご紹介したカフェの初年度平均日販の例で考えてみましょう。カフェの初年度平均日販は、500m内昼間人口だけで決まるのではなく、駅からの距離や席数、視認性(店を視認のしやすいかどうか)などでも変わってきます。これを数式で表わしたのが以下です。

このように、イコールの右辺に2つ以上説明変数がきた場合は、重回帰分析と言います。偏回帰係数は、説明変数の数だけ算出され、予測したい対象と同じ単位(ここでは、「円」)とみることができます。
駅からの距離が100m離れれば、売上は10,877円マイナスになる、席数が1席増えたら209円増える、視認性が1スコア増えると151,328円増える、などと解釈できます。
重回帰分析の式は複雑になりますが、非常に解釈しやすいモデルとなることから、よく利用されます。
4.【ポイント】線形回帰分析は因果関係を前提に行う
線形回帰分析を行う際は、変数の関係が因果関係となっていることを前提にモデルを作成します。
因果関係とは、原因と結果であることが明らかな関係を指します。時間的な前後関係や、一般的に原因と結果であると明らかな関係です。
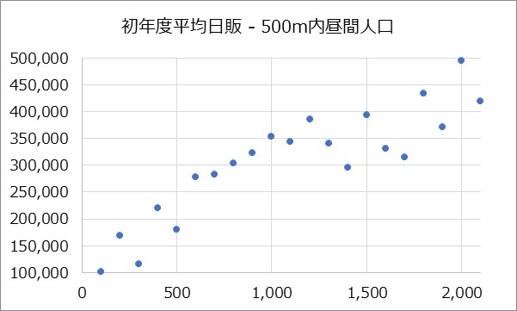
例えば上記の散布図は、カフェの1日の売上を縦軸、半径500m以内の昼間人口を横軸に取りプロットしました。昼間人口が多ければ多いほど、売上が高いことが分かります。人口が多ければ売上が高いという関係は、一般的にも明らかであり、因果関係が明確であると判断できます。
因果関係とよく比較されるのが「相関関係」です。相関関係は、原因と結果であることが明らかではないが、一方の変数の値が大きくなると、他方の値も大きく(小さく)なるような関係です。
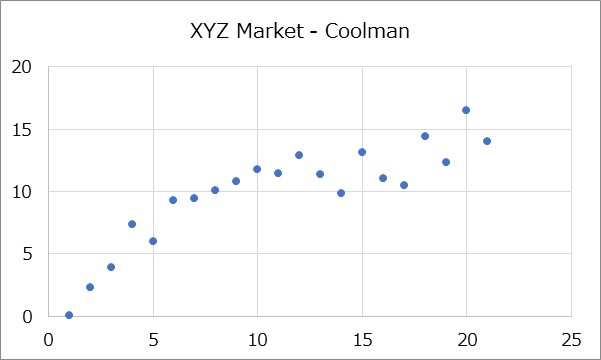
例えば上記の散布図は、ショッピングセンターにある2店舗の1日当たりの売上を表しています。縦軸はXYZ Marketで、横軸はCoolmanで、1日の売上がいくらだったかをプロットしたものです。
XYZ Marketの売上が高い日は、Coolmanの売上も高いということが分かります。
では、これはどちらが原因で、どちらが結果になるでしょうか。XYZ Marketで買い物をしたから、Coolmanでも買い物するのか、それとも逆なのか……。
これは、ショッピングセンターに来た人が多いから、この2店舗で買い物する人が多いという他の原因に基づいています。つまり、この2つの店舗売上は別々の結果ということになります。さらに、来客数が多いだけではなく、この2店舗で買い物をするタイプ(クラスター)の顧客が多かったことが推測されます。この場合、2店舗の売上は、同じ原因に対する2つの事象(結果)なので、相関関係と言えます。
線形回帰分析の場合には、最初に紹介した、因果関係を前提としてモデルを作成します。目的変数と説明変数を取り違えると誤った予測値が出てしまいますので、ご注意ください。
5.最小二乗法による回帰直線の求め方
回帰分析で回帰直線を計算する際に用いられるのが「最小二乗法(英語:least squares method)」です。最小二乗法とは、誤差の伴う測定値の処理において、その予測誤差の2乗の和を最小にすることで最も確からしい関係式を求める方法です。
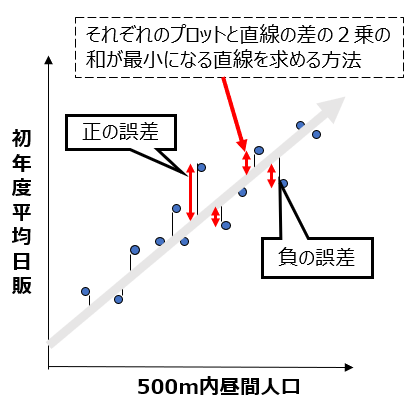
初年度平均日販と半径500m以内の昼間人口の関係を表す散布図を例に考えてみましょう。単回帰分析では、右肩上がりの直線を引くと、散布図のドットに近いところを通ります。この直線の傾きと、切片(横軸が0の時の縦軸の値)が一次方程式では必要になってきます。
どこを通って、どれくらいの傾きを持つかというのを計算するときに、この直線上の予測値(一次方程式で算出)と実際の値には、多かれ少なかれ誤差があります。各データは直線よりも大きい(正の誤差)こともあれば、小さい(負の誤差)こともあるので、そのまま合計すると値のプラス・マイナスで相殺されてしまいます。そこで、この誤差を二乗して足し合わせた合計が最小になるよう、切片と傾きを求めます。
重回帰分析の場合は、計算が複雑にはなりますが、考え方は単回帰分析と同様です。誤差を最小にして最適なモデルを求めます。
6.線形回帰分析の評価基準:決定係数・多重共線性
線形回帰分析の結果を読み取る際に、知っておかなければいけないのが「決定係数(R2)」と「多重共線性」です。それぞれ見ていきましょう。
決定係数(R2)とは
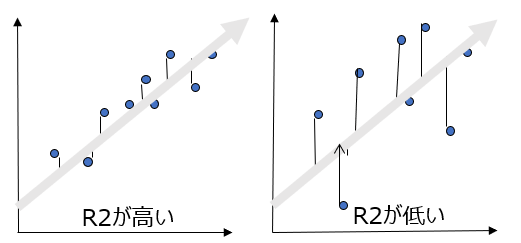
線形回帰分析結果の評価指標の一つとして、分析の精度を示す「決定係数(R2)」があります。決定係数は、予測値と実際の値の当てはまり度合いを表わし、0から1までの値をとります。決定係数が1に近いほど当てはまりがよいと評価します。
【決定係数の評価基準】
分析の精度が非常によい・・・0.8以上
分析の精度がややよい・・・・0.5以上
分析の精度がよくない・・・・0.5未満
多重共線性(multicollinearity)とは
線形回帰分析の説明変数(x)の中に相互に高い相関関係がある場合、多重共線性があるといいます。多重共線性があると偏回帰係数の推定値が不安定になり、分析結果に影響を及ぼす可能性があります。このため、高い相関をもっている変数のどちらかをモデルから除外して重回帰分析を行います。
前述した下記の式を例に見ていきます。

説明変数には、「駅からの距離」「席数」「視認性」「500m内昼間人口」があります。このうち2つの間、または1対多の間で相関が強い場合には、多重共線性の影響を受けます。
例えば、席数が増えたら、当然売上は増えると思いますよね。ところが、席数と昼間人口の相関が高い場合には、席数の偏回帰係数がプラスにならずにマイナスになってしまうといったことが起こりえます。偏回帰係数がおかしいと思った場合には、多重共線性を疑ってみて下さい。
(参考)
※VIF / Variance Inflation Factor 多重共線性を検出するための指標の1つにVIFがあります。値が10より大きい場合はその変数を分析から除いた方がよいと考えられます。
7.まとめ
今回は、「線形回帰分析」の基礎について解説しました。「線形回帰分析」は様々なビジネス課題のヒントを得ることが期待できる分析手法です。
IBM SPSS Modelerを使った「線形回帰分析」については、デモ動画を用意しましたので、あわせてご確認ください。
AITでは、分析プロジェクトの検討段階から、データ準備の支援、モデル開発、ビジネス活用、また人材育成までをトータルにご支援。お客様ご自身が継続的なデータ分析活動を推進できる組織、体制作りのお手伝いをします。
